亲爱的读者，你是否曾在数学课上对“幂函数的定义域”这个概念感到困惑？别担心，今天我要带你一起深入探索这个神秘的世界，让你对这个概念有更清晰的认识。让我们一起揭开幂函数定义域的神秘面纱吧！

一、什么是幂函数？

在数学的世界里，幂函数是一种非常基础的函数类型。它由一个底数和一个指数组成，通常表示为f(x) = x^n，其中x是自变量，n是指数。这个指数n可以是任何实数，但要注意，当n为0时，f(x) = x^0 = 1，这是一个特殊的幂函数。

二、幂函数的定义域

那么，什么是幂函数的定义域呢？简单来说，定义域就是函数中自变量x可以取的所有值的集合。对于幂函数f(x) = x^n，它的定义域取决于指数n的值。

1. 当n为正整数时

当n为正整数时，幂函数的定义域通常是所有非负实数。这是因为，当x为负数时，x^n的结果会变得非常复杂，甚至可能不是实数。例如，f(x) = x^2的定义域就是所有非负实数，因为负数的平方仍然是正数。

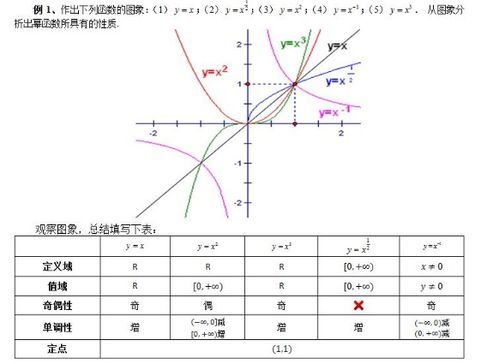
2. 当n为负整数时

当n为负整数时，幂函数的定义域就变得有些特殊了。以f(x) = x^(-1)为例，它的定义域是所有非零实数。这是因为，当x为0时，x^(-1)的结果是无穷大，这在数学上是不允许的。因此，0不能包含在定义域中。

3. 当n为分数时

当n为分数时，幂函数的定义域同样取决于分数的分子和分母。以f(x) = x^(1/2)为例，它的定义域是所有非负实数。这是因为，当x为负数时，x^(1/2)的结果是虚数，这在实数范围内是不存在的。因此，定义域中不能包含负数。

4. 当n为正无理数时

当n为正无理数时，幂函数的定义域通常是所有实数。这是因为，无论x取什么值，x^n的结果都是实数。例如，f(x) = x^(π)的定义域就是所有实数。

5. 当n为负无理数时

当n为负无理数时，幂函数的定义域同样取决于分数的分子和分母。以f(x) = x^(-π)为例，它的定义域是所有非零实数。这是因为，当x为0时，x^(-π)的结果是无穷大，这在数学上是不允许的。因此，0不能包含在定义域中。

三、幂函数定义域的几何意义

幂函数的定义域在几何上有着重要的意义。以f(x) = x^2为例，它的定义域是所有非负实数。在坐标系中，这个函数的图像是一个开口向上的抛物线，顶点位于原点。这意味着，当x取任何非负实数时，函数f(x)都有对应的值。

而对于f(x) = x^(-1)，它的定义域是所有非零实数。在坐标系中，这个函数的图像是一条通过原点的直线，斜率为-1。这意味着，当x取任何非零实数时，函数f(x)都有对应的值。

四、幂函数定义域的应用

幂函数的定义域在数学的各个领域都有广泛的应用。以下是一些例子：

1. 在物理学中，幂函数的定义域可以用来描述物体的运动轨迹。例如，自由落体运动的位移s与时间t的关系可以表示为s = (1/2)gt^2，其中g是重力加速度，t是时间。这个函数的定义域是所有非负实数。

2. 在经济学中，幂函数的定义域可以用来描述市场需求。例如，某种商品的需求量Q与价格P的关系可以表示为Q = kP^(-α)，其中k和α是常数。这个函数的定义域是所有非零实数。

3. 在生物学中，幂函数的定义域可以用来描述生物种群的增长。例如，某种生物种群的数量N与时间t的关系可以表示为N = N0e^(rt)，其中N0是初始种群数量，r是增长率，t是时间。这个函数的定义域是所有实数。

通过本文的介绍，相信你对幂函数的定义域有了更深入的了解。在数学的世界里，幂函数的定义域是一个非常重要的概念，它不仅影响着函数的性质，还与实际应用密切相关。希望这篇文章能帮助你更好地理解幂函数的定义域，让你在数学的道路上越走越远。